...zur Hauptseite 
Dreiteilung des Winkels?
Natürlich tauchen immer wieder angebliche Lösungen zur Dreiteilung des Winkels mit Zirkel und Lineal auf.
Die älteste bekannte Lösung stammt von Archimedes (um 287 v. Chr.). Diese Konstruktion ist zwar vollkommen exakt hinsichtlich der Winkelwerte, aber leider hat Archimedes dabei die Regeln nicht eingehalten. Er benutzte ein markiertes Lineal und das war nicht erlaubt.
Eine weitere Lösung benutzt den Tomahawk, ein geometrisches Werkzeug, das mittels Zirkel und Lineal konstruiert werden kann. Die eigentliche Dreiteilung besteht aber darin, dieses Werkzeug geschickt an einen vorgegebenen Winkel anzulegen. Ähnlich wie bei Archimedes verstößt dies gegen die klassischen Regeln.
Bei den sonst bekannten Konstruktionen handelt es sich immer um Näherungen, keine exakten Lösungen im Sinne der klassischen Regeln. Im Jahre 2007, als ich diese Internetseite erstmals erstellte, fand ich eine gute Näherungslösung (www.balavat.de/mathematik_dreiteilung.php).
Diese produziert einen Fehler, der geringer als 0,05 Grad ist, und zwar bezogen auf die Abweichung des mittleren von den beiden äußeren Winkeln. Ich habe das einmal mit dem hervorragenden Programm "Zirkel und Lineal (Z. u. L.)" nachvollzogen, wie das folgende Bild zeigt:
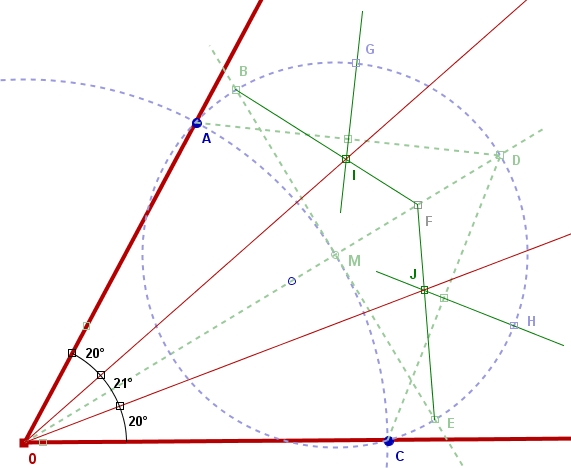
Die mit der Software gemessenen Winkel betragen:
W1 = 20,46416 Grad
W2 = 20,50528 Grad
W3 = 20,46416 Grad
Im Frühjahr/Sommer 2012 sandte mir Peter Katzlinger eine sehr gute Näherungslösung zu, deren Grundprinzip im folgenden Bild auszugsweise dargestellt ist.
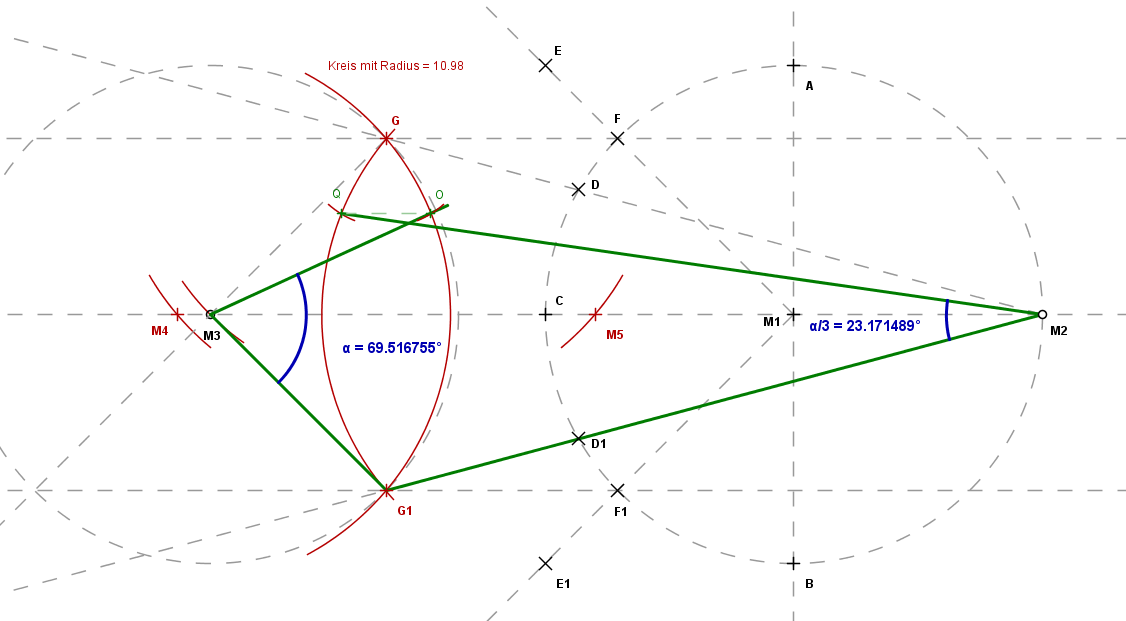Größeres Bild ...
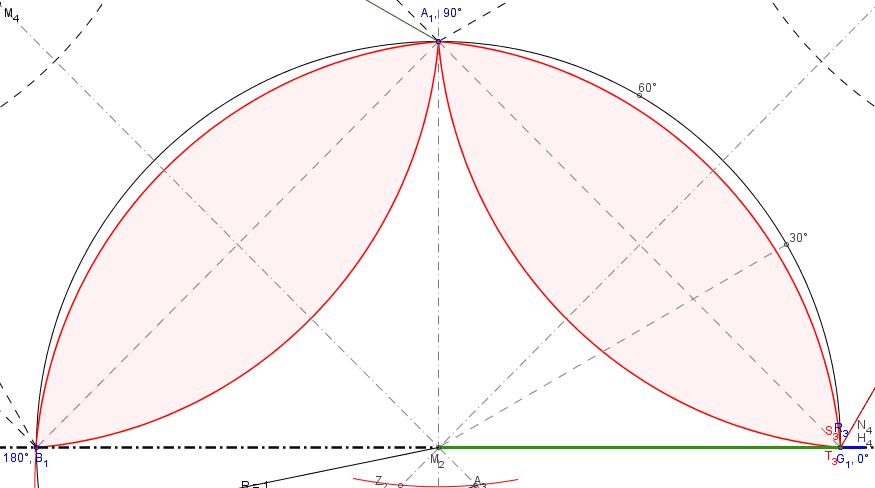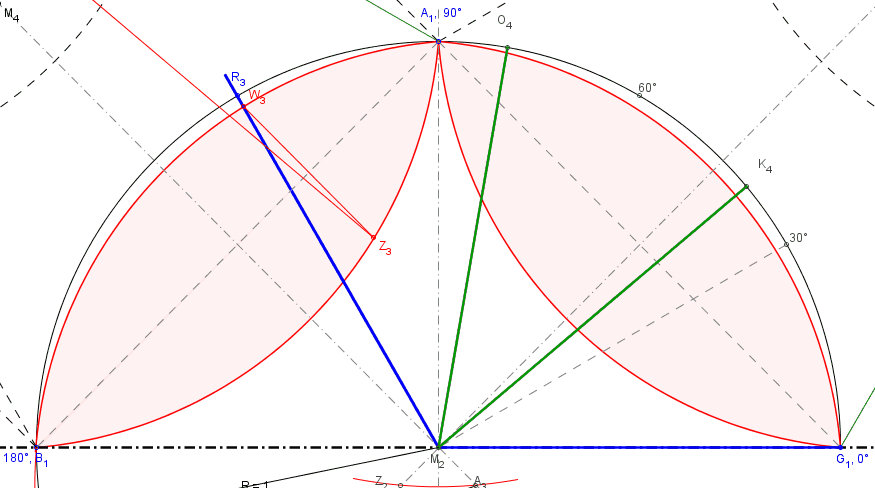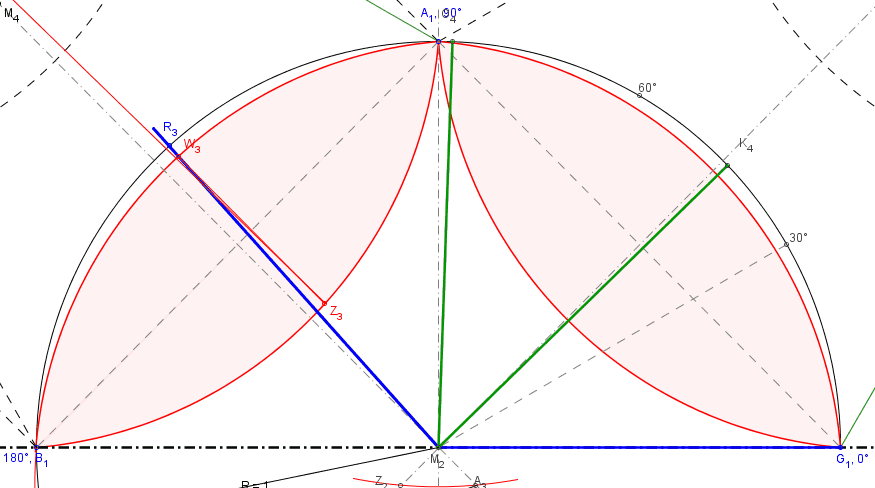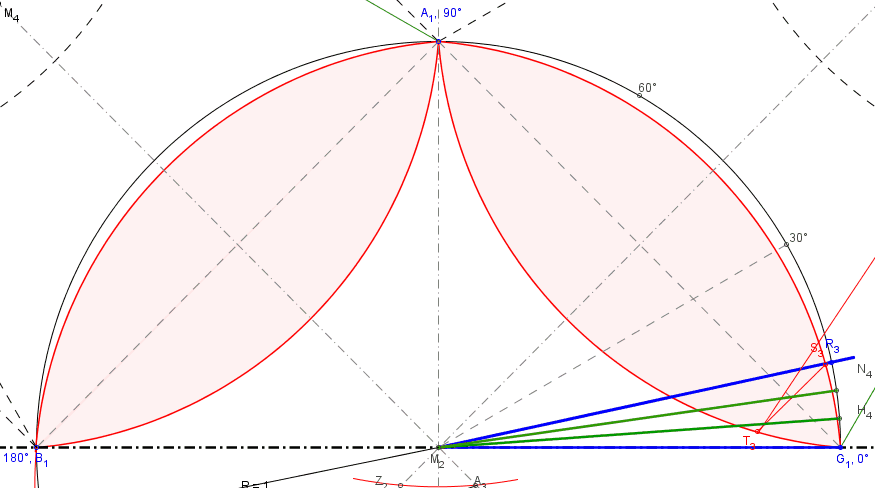Im dargestellten Beispiel weicht der annähernd gedrittelte Winkel nur um 0,00076 Grad vom idealen Drittelwinkel ab. Das gilt zwar nicht für alle Winkel, jedoch tritt im ungünstigsten Fall eine Abweichung von etwa 0,0018 Grad auf, also besser als 6,5 Bogensekunden. Das wären bei einem Radius von 1 Kilometer nur 3,15 cm Abweichung.
Dabei fand ich das Konstruktionsprinzip (Linsenprinzip) sehr einfach und klar. Eine bewegliche Konstruktion für Winkel bis zu 180 Grad finden Sie hier (mit GeoGebra konstruiert).
Inzwischen hat Peter Katzlinger noch weitere Konstruktionen ausprobiert und auf GeoGebraTube veröffentlicht. Darunter ist auch eine weitere interessante Dreiteilung. Dazu eine kleine Geschichte: Nachdem es ihm gelungen war, auf einer Strecke eine Näherung der Kreiszahl Pi darzustellen, grübelte er nach, wie man daraus vielleicht "Die Dreiteilung des Winkels" ableiten könnte. Er nahm 1/4 der angenäherten Pi-Strecke, zerlegte den Winkel 45° in gleiche Kreissektoren, teilte die geviertelte ca. Pi-Strecke (Anzahl gleich den Kreissektoren) und verband die gefundenen Schnittpunkte zwischen den Winkelhalbierenden und den Streckenhalbierenden mittels Kreisbogen. So kam er auf die Pi/4-Quadratrix, ohne von der Quadratrix des Hippias zu wissen.
...zurück zum Text
Letztes Update dieser Seite: 9. März 2021