...zur Hauptseite 
Mathematik
Kein Buch mit sieben Siegeln
sollte man sich von dem Problem lösen.
Das gilt zwar nicht immer, jedoch hier bestimmt:
Die klassischen mathematischen Probleme
In der griechischen Antike beschäftigten sich die meisten klassischen Probleme mit Geometrie. Damals war die Algebra noch nicht so weit entwickelt. Für alle Probleme galt die Lösungsbedingung, dass als Hilfsmittel nur Stift, Zirkel und Lineal verwendet werden durften. Die wichtigsten dieser alten Probleme waren:- Die Konstruktion eines Quadrats, das den gleichen Flächeninhalt wie ein gegebener Kreis hat
("Quadratur des Kreises"). - Die Teilung eines beliebigen Winkels in drei gleich große Teile
("Dreiteilung des Winkels"). - Die Konstruktion eines Würfels, der genau das doppelte Volumen besitzt wie ein vorgegebener Würfel
("Verdoppelung des Würfels").
Aber wie steht's mit folgendem Rätsel?
Das Puzzle
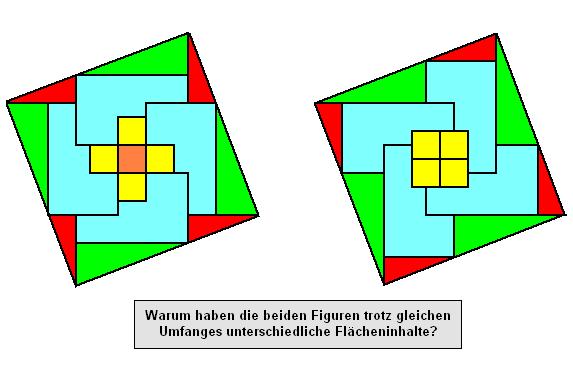
Die beiden Figuren bestehen aus den genau gleichen Puzzleteilen. Nur wird bei der rechten Figur ein Teil weniger gebraucht. Ist es in der 4. Dimension verschwunden? Oder gibt es eine banale Erkärung?
Einen Lösungshinweis gibt es hier ...
Die Erbschaft
Es war einmal ein Bauer, der hatte 3 Söhne. Als er nun bald sterben musste, sagte er zu ihnen: "Ich vermache euch meine 17 Kühe. Davon soll der Älteste die Hälfte bekommen, der Mittlere ein Drittel und der Jüngste ein Neuntel."Nach seinem Tode überlegten sich die Söhne lange, wie sie diese merkwürdige Teilung bewerkstelligen sollten. Schließlich konnten sie ja die Kühe nicht zerschneiden.
Irgendwann fragten sie ihren klugen Nachbarn. Der lachte bloß und bald war die Teilung erledigt. Wie hat er das gemacht?
Die Datteln
Es waren einmal zwei Araber, die durch die Wüste wanderten. Sie hatten nur noch einige Datteln zur Wegzehrung: Achmed hatte noch 5 und Omar nur noch 3 Datteln. Da begegnete ihnen ein Wanderer. Es war ein reicher Mann, der sich verirrt hatte. Er hatte überhaupt nichts mehr zu essen. So wanderten sie gemeinsam weiter und teilten ihre Datteln gerecht miteinander.
Als sie an einer Oase angekommen waren, verabschiedeten sie sich und der Reiche schenkte den beiden zum Dank 8 Goldstücke.
Achmed und Omar fingen jedoch an, sich zu streiten, wie sie die Goldstücke teilen sollten. Achmed meinte: "Da ich 5 Datteln hatte und du 3, bekomme ich natürlich 5 Goldstücke und du 3." Aber Omar sagte: "Wir sind 2 Personen, also stehen jedem von uns 4 Goldstücke zu."
Schließlich gingen die beiden zu einem weisen Derwisch und baten ihn um eine gerechte Entscheidung. Dieser sagte aber: "Ihr seid beide im Unrecht, denn Achmed muss für seine 5 Datteln 7 Goldstücke erhalten, Omar jedoch nur eines."
Wie ist diese Entscheidung zu begründen?