Spruch des Monats
In einem dankbaren Herzen herrscht ewiger Sommer.
Celia Layton Thaxter (1835 - 1894)

Zitate und Weisheiten
„Seit man begonnen hat, die einfachsten Behauptungen zu beweisen, erwiesen sich viele von ihnen als falsch.“
Bertrand Russell (1872 – 1970)
„Zuerst ignorieren sie dich, dann lachen sie über dich, dann bekämpfen sie dich und dann gewinnst du.“
Wird oft Mahatma Ghandi zugeschrieben, ist aber von Nicholas Klein in einer Rede von 1918 verwendet worden:
„Und, liebe Freunde, in dieser Geschichte findet ihr die Historie unserer gesamten Bewegung wieder: Zuerst ignorieren sie dich. Dann machen sie dich lächerlich. Dann greifen sie dich an und wollen dich verbrennen. Und dann errichten sie dir Denkmäler. Und das ist genau das, was den vereinigten Arbeitern der Bekleidungsindustrie Amerikas passieren wird.“
"Wer den anderen liebt,
lässt ihn gelten,
so wie er ist,
wie er gewesen ist
und wie er sein wird."
Albert Camus
Kein bequemer und ruhiger Zustand,
sondern ein großes und wunderbares Abenteuer."
Antoine de Saint-Exupery
"Der Maßstab für Fortschritt ist nicht, wie viel wir dem Überfluss derjenigen hinzufügen, die ohnehin schon genug besitzen, sondern ob es gelingt, denjenigen, die zu wenig besitzen, das zu geben, was sie zum Leben brauchen."
Franklin Delano Roosevelt (1882 – 1945)
32. Präsident der USA
"Liebe zur Natur ist die einzige Liebe, die menschliche Hoffnungen nicht enttäuscht."
Honoré de Balzac (1799 – 1850)
"Der Wunsch nach Vollkommenheit ist die schrecklichste Krankheit, die je den menschlichen Geist befallen hat."
Theodor Fontane
"Das Unglück des Menschen beginnt dann, wenn er außerstande ist, mit sich allein in einem Zimmer zu bleiben."
Blaise Pascal
"Wer glaubt, ein Christ zu sein, weil er die Kirche besucht, irrt sich.
Man wird ja auch kein Auto, wenn man in eine Garage geht."
Albert Schweitzer
"Man muß das Wahre immer wiederholen, weil auch der Irrtum um uns her immer wieder gepredigt wird und zwar nicht von einzelnen, sondern von der Masse, in Zeitungen und Enzyklopädien, auf Schulen und Universitäten. Überall ist der Irrtum obenauf, und es ist ihm wohl und behaglich im Gefühl der Majorität, die auf seiner Seite ist."
Johann Wolfgang von Goethe
(1749 - 1832), deutscher Dichter der Klassik, Naturwissenschaftler und Staatsmann
"Die Freiheit des Menschen liegt nicht darin, daß er tun kann, was er will, sondern das er nicht tun muß, was er nicht will."
Jean-Jacques Rousseau
(* 28. Juni 1712 in Genf, † 2. Juli 1778 in Ermenonville bei Paris)
"Freiheit ist immer die Freiheit der Andersdenkenden, sich zu äußern."
Rosa Luxemburg
"Handle so, dass die Maxime Deines Willens jederzeit zugleich als Prinzip einer allgemeinen Gesetzgebung gelten könne."
Imanuel Kant (1724 – 1804)
Eine Form seines Kategorischen Imperatives
"Die billigste Art des Stolzes ist hingegen der Nationalstolz. Denn er verrät in dem damit Behafteten, den Mangel an individuellen Eigenschaften, auf die er stolz sein könnte, indem er sonst nicht zu dem greifen würde, was er mit so vielen Millionen teilt. Wer bedeutende persönliche Vorzüge besitzt, wird vielmehr die Fehler seiner eigenen Nation, da er sie beständig vor Augen hat, am deutlichsten erkennen. Aber jeder erbärmliche Tropf, der nichts in der Welt hat, auf das er stolz sein könnte, ergreift das letzte Mittel, auf die Nation, der er gerade angehört, um stolz zu sein."
Arthur Schopenhauer (1788 – 1860)
"Was ist Nationalismus? Das ist ein Patriotismus, der seine Vornehmheit verloren hat."
Albert Schweitzer (1875 – 1965)
"Wer die Welt verbessern will, kann gleich bei sich selber anfangen."
Astrid Lindgren
"Ihre Meinung ist mir zwar widerlich, aber ich werde mich dafür tot schlagen lassen, dass Sie sie sagen dürfen."
François Marie Arouet genannt Voltaire (1694 – 1778)
"Ich stimme mit dem was Sie sagen nicht überein, werde aber bis zum Tode Ihr Recht es zu äußern verteidigen."
"I disapprove of what you say, but I will defend to the death your right to say it."
Wird in diesem Wortlaut wohl zu unrecht Voltaire zugeschrieben.
"Monsieur l'abbé, I detest what you write, but I would give my life to make it possible for you to continue to write."
aus einem Brief an Monsieur le Riche, 6. Februar 1770.
Das obige Zitat stammt von Evelyn Beatrice Hall, die es unter dem Pseudonym Stephen G Tallentyre in The Friends of Voltaire (1906) verwendet.
Besondere Weisheiten
Als kleine Hilfe in großen LebenskrisenWichtig ist nur, dass du wieder aufstehst.
Gandhis 10 Weisheiten um die Welt zu verändern
zitert nach STREETWORKER I/2009"Auge um Auge führt nur zur Erblindung der ganzen Welt."
"Es ist nicht weise zu sicher über seine eigene Weisheit zu sein. Es ist gesund daran erinnert zu werden, dass die Starken schwach werden und die Weisen sich irren."
"Der Mensch wird großartig in dem Maße, wie er für das Wohlergehen seiner Mitmenschen agiert."
"Ich meine, Führung wurde zu einer Zeit mit Kraft gleichgesetzt; aber heute bedeutet es, wie man mit den Menschen auskommt."
"Ziele immer auf eine völlige Harmonie deiner Gedanken, Worte und Taten. Versuche deine Gedanken zu reinigen und alles wird gut."
Letztes Update: 16. April 2018
Das Phänomen von Hanns Dieter Hüsch
Was ist das für ein Phänomen
Fast kaum zu hören kaum zu sehn
Ganz früh schon fängt es in uns an
Das ist das Raffinierte dran
Als Kind hat man’s noch nicht gefühlt
Hat noch mit allen schön gespielt
Das Dreirad hat man sich geteilt
Und niemand hat deshalb geheult
Doch dann hieß es von oben her
Mit dem da spielst du jetzt nicht mehr
Das möcht ich nicht noch einmal sehn
Was ist das für ein Phänomen
Und ist man größer macht man’s auch
Das scheint ein alter Menschenbrauch
Nur weil ein andrer anders spricht
Und hat ein anderes Gesicht
Und wenn man’s noch so harmlos meint
Das ist das Anfangsbild vom Feind
Er passt mir nicht er liegt mir nicht
Das ist das nicht und find ihn schlicht
Geschmacklos und hat keinen Grips
Und außerdem sein bunter Schlips
Dann setzt sich in Bewegung leis’
Der Hochmut und der Teufelskreis
Und sagt man was dagegen mal
Dann heißt’s: Wer ist denn hier normal
Ich oder er du oder ich
Ich find den Typen widerlich
Und wenn du einen Penner siehst
Der sich sein Brot vom Dreck aufliest
Dann sagt ein Mann zu seiner Frau
Guck dir den Schmierfink an die Sau
Verwahrlost bis zum dorthinaus
Ja früher warf man die gleich raus
Und heute muss ich sie ernähr’n
Und unsereins darf sich nicht wehr’n
Und auch die Gastarbeiterpest
Der letzte Rest vom Menschenrest
Die sollt man alle das tät gut
Spießruten laufen lassen bis auf’s Blut
Das hamwer doch schon mal gehört
Da hat man die gleich streng verhört
Verfolgt gehetzt und für und für
Ins Lager reingepfercht und hier
Hat man sie dann erschlagen all
Die Kinder mal auf jeden Fall
Die hatten keinem was getan
Was ist das für ein Größenwahn
das lodert auf im Handumdrehn
Und ist auf einmal Weltgeschehn
Denn plötzlich steht an jedem Haus
Die Juden und Zigeuner raus
Nur weil kein Mensch derselbe ist
Und weiß und schwarz und gelbe ist
Wird er verbrannt ob Frau ob Mann
Und das fängt schon von klein auf an
Und wenn ihr heute Dreirad fahrt
Ihr Sterblichen noch klein und zart
Es ist doch eure schönste Zeit
voll Phantasie und Kindlichkeit
Lasst keinen kommen der da sagt
Dass ihm dein Spielfreund nicht behagt
Dann stellt euch vor das Türkenkind
dass ihm kein Leids und Tränen sind
Dann nehmt euch alle an die Hand
Und nehmt auch den der nicht erkannt
Dass früh schon in uns allen brennt
Das was man den Faschismus nennt
Nur wenn wir eins sind überall
Dann gibt es keinen neuen Fall
Von Auschwitz bis nach Buchenwald
Und wer’s nicht spürt der merkt es bald
Nur wenn wir in uns alle sehn -
Besiegen wir das Phänomen
Nur wenn wir alle in uns sind -
Fliegt keine Asche mehr im Wind
(Hanns Dieter Hüsch)
Weiterführende Links:

Weiterführende Links:

Weiterführende Links:
Weiterführende Links:
Besondere Links (öffnen im Neuen Fenster):
Politik ist mehr ...

Weiterführende Links:
„Nicht die Hirne und Hände, sondern die Mäuler bringen das meiste Unheil über die Menschen.“
B. Traven

Religion - Fanatismus oder Nächstenliebe?
Gibt es eine einzig wahre Religion?
Dazu einige Stimmen:Der säkulare Weg
Frieden ist der Weg
Mahatma Gandhi
Solidarität
Ich wollte deshalb eine Gemeinschaft, in der die menschliche Solidarität gilt, unabhängig von allen Konfessionen“
Roger Schutz
Weiterführende Links:
Ausgewählte Texte:
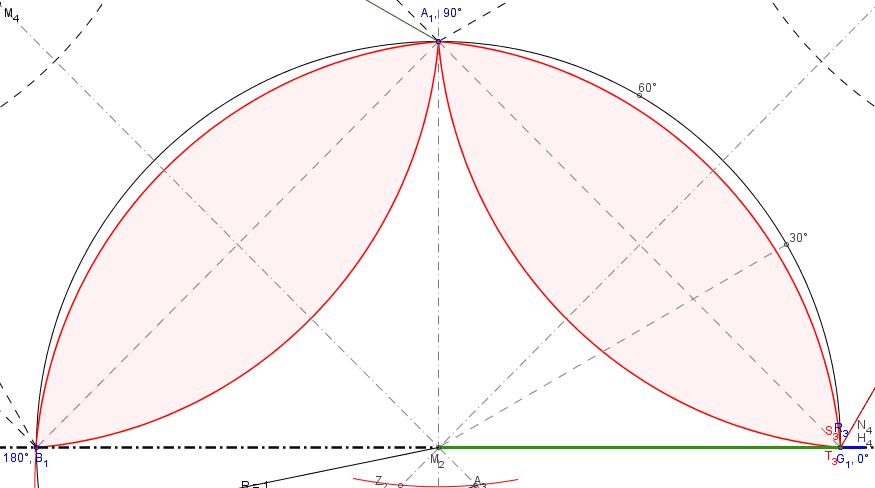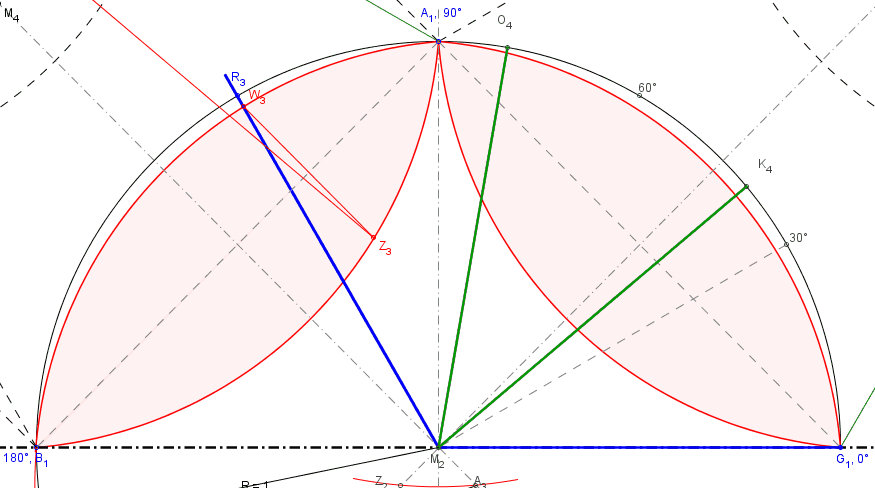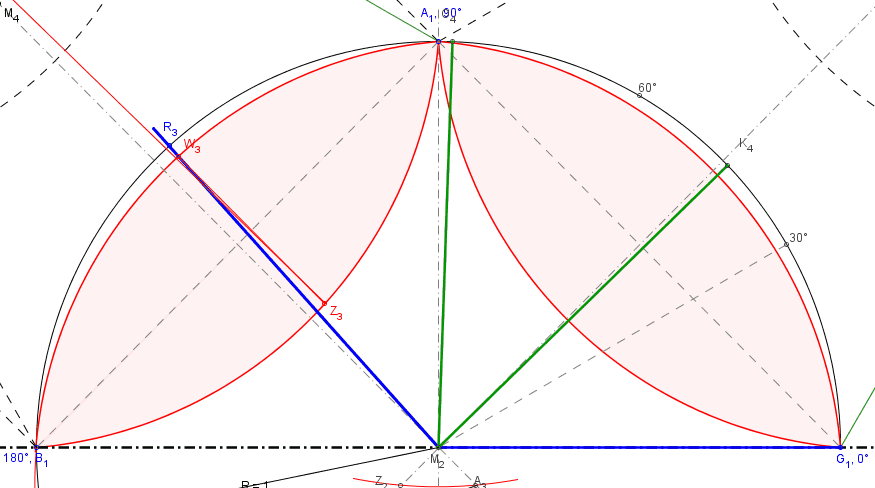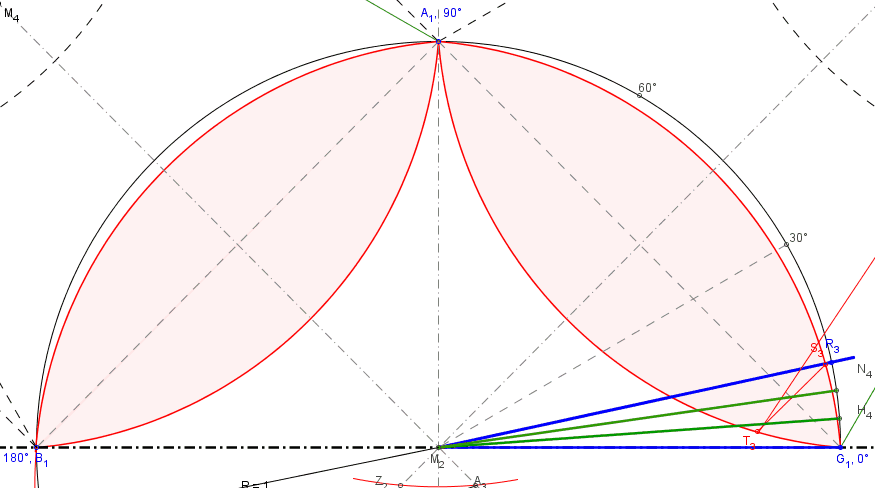
Mathematik und Denksport
Für die Fans der Unterhaltungsmathematik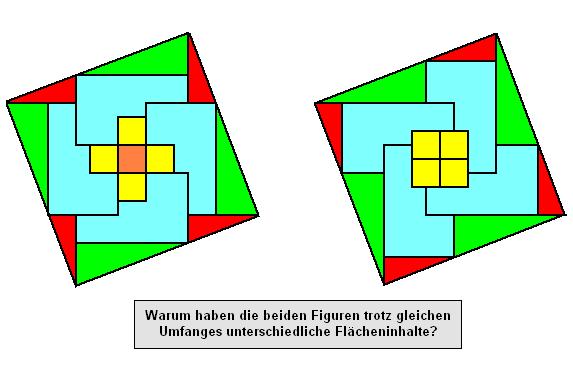

Weiterführende Links:
Weiterführende Links: